ボールを打つアイコンのドラッグ速度と到達位置の計算

　ゴルフゲームの制作において、ボールを打つアイコンのドラッグスピードとボールがゲームビュー画面上で飛ぶ距離の関係を把握する必要がありました。
　

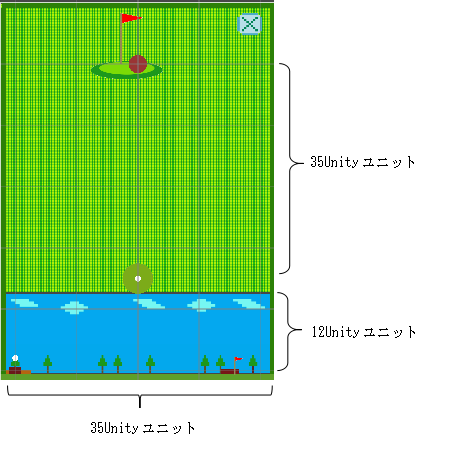
　ゴルフゲームでは、Size:50とし、画面上に表示されているマス目１つは10Unityユニット、スタート位置からカップまでの距離は約35mとします。

　そこで、重力だけを考慮した放物線のカーブを表わす２次方程式を解くことでアイコンのドラッグスピードを決めました。
　ゴルフのカップまでの距離は３５ｍ、高さは１２ｍとし、このスペースの中でボールが移動するためのドラッグスピードとボールに与える初速度を求めます。

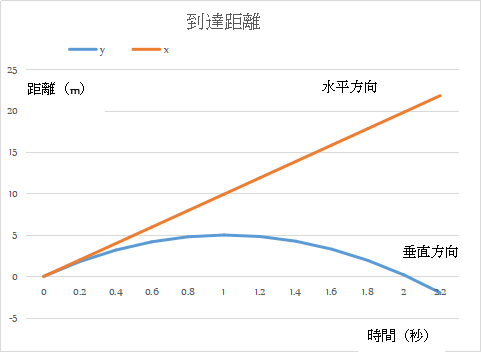
　ボールには重力のみが働くものとし、ボールの垂直方法、水平方向の運動式を下記に示します。
（垂直方向）
　垂直方向の速度　\(ｖy＝v0・sin(θ)ーg・t\)
　ここで、V0は初速度(m/s)、θはx軸に対する角度（ラジアン）、tは時間（秒）、gは重力の加速度\((s/m^2)\)です。
　この式を積分して垂直方向の位置ｙは、
　\(y＝y0＋v0・sin(θ)・tー(g/2)・t^2\)
　ここで、y0は初期位置です。
（水平方向）
　水平方向の速度　\(vx＝v0・cos(θ)\)
　水平方向の距離　\(x＝v0・cos(θ)・t\)

　初速度(V0)を14m/s、角度45°でボールを打ったときの最高地点は、垂直方向の速度が0m/sとなるときで、その時間tは1秒となり、高さは約5m、到達距離は約20mとなります。
　ここで、ゲームスペース内に収まるようにするために、初速度14m/sとするためのプレイヤーアイコンのドラッグスピードを調整します。
　スマホ画面上の横幅35Unityユニット（35ｍ）の5分の1（7ｍ）を使って0.5秒でドラッグすると初速度の14m/sになります。
　ボールを打つドラッグ時間0.5秒は長いため、0.1秒ぐらいの間隔でドラッグして、そのドラッグにかかった時間を5倍して、ボールに初速度を与えるようにしました。

currentSpeed = (currentPosition - lastPosition) / (dragTime * 5);