目次
１．NumPyのメソッド
（１）np.array()
（２）np.zeros()
２．ndarray（N-dimensional arrayの略）
（１）ndarray.shape
（２）ndarray.dtype
（３）ndarray.reshape()
（４）ndarray.flatten()
（５）ndarray.sum()
（６）ndarray.mean()
（７）ndarray.max() と ndarray.min()
（８）ndarray.dot()
（９） ndarray.transpose()
３．ベクトルの類似性の評価
３．１ 内積
（１）行ベクトル間の内積
（２）列ベクトル間の内積
３．２ コサイン類似度
４．コレクションデータ型とメソッド
４．１ リスト (List)
４．２ タプル (Tuple)
４．３ セット (Set)
４．４ ディクショナリ (Dictionary)
４．５ デフォルトディクショナリ (defaultdict)
５．データ構造の操作
５．１ インデックス参照（スライス）
（１）リストのスライス
（２）文字列のスライス
（３）１次元配列のスライス
（４）２次元配列のスライス
（５）３次元配列のスライス
（６）スライスオブジェクト
１．NumPyのメソッド
（１）np.array()
多次元配列を作成します。
|
1 2 3 4 5 6 |
import numpy as np array1 = np.array([1, 2, 3, 4, 5]) array2 = np.array([[1, 2, 3], [4, 5, 6]]) print("array1:",array1) # [1 2 3 4 5] print("array2:",array2) #array2: [[1 2 3][4 5 6]] |
（２）np.zeros()
全ての要素がゼロで初期化された新しい配列を生成します。この関数は、配列の形状とデータ型を指定して、必要なサイズのゼロ配列を作成します。
ａ）1次元配列の生成
|
1 2 3 4 5 6 |
# -*- coding: utf-8 -*- import numpy as np # 要素数が5の1次元配列を生成 array = np.zeros(5) print(array) # 出力: [0. 0. 0. 0. 0.] |
ｂ）2次元配列の生成
|
1 2 3 4 5 6 7 8 9 |
# -*- coding: utf-8 -*- import numpy as np # 2x3の2次元配列を生成 array = np.zeros((2, 3)) print(array) # 出力: # [[0. 0. 0.] # [0. 0. 0.]] |
ｃ）データ型を指定する
dtype 引数を使用して配列のデータ型を指定できます。デフォルトでは、float64 型になりますが、整数型や他の型を指定することもできます。
|
1 2 3 4 5 6 7 |
# -*- coding: utf-8 -*- import numpy as np # 要素数が5の整数型（int）の1次元配列を生成 array = np.zeros(5, dtype=int) print(array) # 出力: [0 0 0 0 0] |
（３）np.pad()
np.pad()は、NumPy配列にパディング（追加の要素）を付けるための関数です。パディングは、配列の周りに一定の値や特定の方法で追加される要素です。これにより、配列のサイズを増やすことができます。
基本的な構文
numpy.pad(array, pad_width, mode, **kwargs)
ここで、
・array：配列
・pad_width：各軸ごとのパディングする量。
pad_width=[((before_1, after_1), … (before_N, after_N))]
(before_i, after_i) は axis=i の index=0 側に before_i、index=-1 側
に after_i だけパディングすることを意味します
・mode：constant 標準、edge 端の値をコピーなど
・**kwargs：オプション
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
# -*- coding: utf-8 -*- import numpy as np array = np.array([[1, 2], [3, 4]]) #一定値でのパディング padded_array = np.pad(array, pad_width=((1, 1), (1, 1)), mode='constant', constant_values=0) print(padded_array) #[[0 0 0 0] # [0 1 2 0] # [0 3 4 0] # [0 0 0 0]] #エッジの値でのパディング padded_array = np.pad(array, pad_width=((1, 1), (1, 1)), mode='edge') print(padded_array) #[[1 1 2 2] # [1 1 2 2] # [3 3 4 4] # [3 3 4 4]] #反射モードでのパディング padded_array = np.pad(array, pad_width=((1, 1), (1, 1)), mode='reflect') print(padded_array) #[[4 3 4 3] # [2 1 2 1] # [4 3 4 3] # [2 1 2 1]] #ラップアラウンドモードでのパディング padded_array = np.pad(array, pad_width=((1, 1), (1, 1)), mode='wrap') print(padded_array) #[[4 3 4 3] # [2 1 2 1] # [4 3 4 3] # [2 1 2 1]] #オプション #mode に応じて追加のキーワード引数が使用 #(例)'constant' モードで constant_values キーワード引数 padded_array = np.pad(array, pad_width=((1, 1), (1, 1)), mode='constant', constant_values=5) print(padded_array) #[[5 5 5 5] # [5 1 2 5] # [5 3 4 5] # [5 5 5 5]] |
２．ndarray（N-dimensional arrayの略）
NumPyではPythonのリストではなく、効率性などからndarrayという独自のデータ構造を演算に使う。
同じ属性や大きさを持った要素を持つ多次元配列を扱うためのクラスの1つ
NumPy では Python の標準機能であるリスト型変数ではなく、NumPyのndarray型という特別な配列を使用し、これにより行列の掛け算、逆行列、固有値などの計算を高速に行うことができる。
ndarrayが持つ属性
(ndarrayのインスタンス変数名).(属性)でndarrayインスタンスの情報を取得することができる。
ndarrayクラスには、データ操作や計算に役立つ多くのメソッドが用意されています。以下に、いくつかの主要なメソッドを紹介します。
属性
ndarray.shape: 配列の形状を表すタプル。
ndarray.dtype: 配列の要素のデータ型。
ndarray.size: 配列の要素の総数。
ndarray.ndim: 配列の次元数。
メソッド
ndarray.astype(dtype): 配列の要素のデータ型を指定された型に変換した新しい配列を返す。
ndarray.copy(): 配列のコピーを作成して返す。
ndarray.flatten(): 配列を1次元にフラット化した新しい配列を返す。
ndarray.reshape(shape): 配列の形状を変更した新しい配列を返す。
ndarray.transpose(*axes): 配列の軸を並べ替えた新しい配列を返す。
ndarray.sum(axis=None): 配列要素の合計を返す。
ndarray.mean(axis=None): 配列要素の平均を返す。
ndarray.min(axis=None): 配列要素の最小値を返す。
ndarray.max(axis=None): 配列要素の最大値を返す。
ndarray.argmin(axis=None): 配列要素の最小値のインデックスを返す。
ndarray.argmax(axis=None): 配列要素の最大値のインデックスを返す。
ndarray.cumsum(axis=None): 配列要素の累積和を返す。
ndarray.cumprod(axis=None): 配列要素の累積積を返す。
（１）ndarray.shape
NumPyの配列（ndarray）オブジェクトの形状を取得します。各次元のサイズを表すタプルが返されます。
|
1 2 3 4 5 6 7 8 |
import numpy as np array1 = np.array([1, 2, 3, 4, 5]) array2 = np.array([[1, 2, 3], [4, 5, 6]]) print("array1:",array1) # [1 2 3 4 5] print("array1.shape:",array1.shape) # (5,) print("array2:",array2) #array2: [[1 2 3][4 5 6]] print("array2.shape:",array2.shape) # (2,3) |
（２）ndarray.dtype
配列のデータ型を取得します。
|
1 2 3 4 |
import numpy as np array = np.array([1, 2, 3]) print("array.dtype",array.dtype) # int64 |
（３）ndarray.reshape()
配列の形状を変更します。元のデータは保持されますが、形状が変わります。
（元の配列）
array = np.array([1, 2, 3, 4, 5, 6])
（変更後の配列）
reshaped_array [[1 2 3]
[4 5 6]]
|
1 2 3 4 5 6 7 |
import numpy as np array = np.array([1, 2, 3, 4, 5, 6]) reshaped_array = array.reshape((2, 3)) print("reshaped_array:",reshaped_array) # [[1 2 3] # [4 5 6]] |
（４）ndarray.flatten()
多次元配列を１次元に変換します。
|
1 2 3 4 5 6 |
import numpy as np array = np.array([[1, 2, 3], [4, 5, 6]]) flattened_array = array.flatten() print("flattened_array",flattened_array) # [1 2 3 4 5 6] |
（５）ndarray.sum()
配列の全要素の合計を計算します。軸を指定することで、その軸に沿った合計も求められます。
|
1 2 3 4 5 6 7 8 9 10 11 |
import numpy as np array = np.array([[1, 2, 3], [4, 5, 6]]) total_sum = array.sum() print("total_sum:",total_sum) # 21 column_sum = array.sum(axis=0) print("column_sum:",column_sum) # [5 7 9] row_sum = array.sum(axis=1) print("row_sum:",row_sum) # [ 6 15] |
（６）ndarray.mean()
配列の全要素の平均を計算します。軸を指定することで、その軸に沿った平均も求められます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
import numpy as np array = np.array([[1, 2, 3], [4, 5, 6]]) total_mean = array.mean() print("total_mean:",total_mean) # 3.5 column_mean = array.mean(axis=0) print() # [2.5 3.5 4.5] print("column_mean:",column_mean) # [2.5 3.5 4.5] row_mean = array.mean(axis=1) print("row_mean:",row_mean) # [2. 5.] |
（７）ndarray.max() と ndarray.min()
配列の最大値と最小値を取得します。軸を指定することで、その軸に沿った最大値と最小値も求められます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import numpy as np array = np.array([[1, 4, 8], [2, 5, 6]]) max_value = array.max() print("max_value:",max_value) # 8 min_value = array.min() print("min_value:",min_value) # 1 column_max = array.max(axis=0) print("column_max:",column_max) # [2 5 8] row_min = array.min(axis=1) print("row_min:",row_min) # [1 2] |
（８）ndarray.dot()
行列のドット積（内積）を計算します。
|
1 2 3 4 5 6 7 8 9 10 11 |
import numpy as np a = np.array([[1, 2], [3, 4]]) b = np.array([[5, 6], [7, 8]]) dot_product = a.dot(b) print("dot_product",dot_product) #[[1*5+2*7 1*6+2*8] #[3*5+4*7 3*6+4*8]] # #[[19 22] # [43 50]] |
（９） ndarray.transpose()
配列の転置を返します。行と列を入れ替えます。
|
1 2 3 4 5 6 7 8 |
import numpy as np array = np.array([[1, 2, 3], [4, 5, 6]]) transposed_array = array.transpose() print("transposed_array:",transposed_array) # [[1 4] # [2 5] # [3 6]] |
３．ベクトルの類似性の評価
３．１ 内積
（１）行ベクトル間の内積
行列aと行列bの各行ベクトル間の内積を計算する方法を示します。
|
1 2 3 4 5 6 7 8 9 |
# -*- coding: utf-8 -*- import numpy as np a = np.array([[1, 2], [3, 4]]) b = np.array([[5, 6], [7, 8]]) # 各行ベクトル間の内積を計算する dot_products = np.dot(a, b.T) print(dot_products) |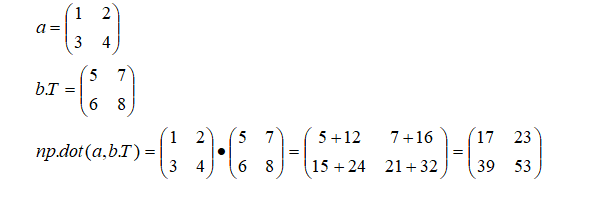
（２）列ベクトル間の内積
行列aと行列bの各行ベクトル間の内積を計算する方法を示します。
|
1 2 3 4 5 6 7 8 9 |
# -*- coding: utf-8 -*- import numpy as np a = np.array([[1, 2], [3, 4]]) b = np.array([[5, 6], [7, 8]]) # 各行ベクトル間の内積を計算する dot_products = np.dot(a.T, b) print(dot_products) |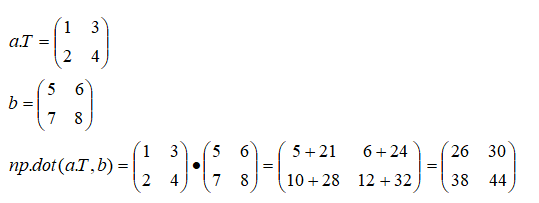
３．２ コサイン類似度
ベクトルのノルム（ユークリッドノルム）
デフォルトでは、np.linalg.norm() はユークリッドノルム（L2ノルム）を計算します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# -*- coding: utf-8 -*- import numpy as np # ベクトルの定義 A = np.array([1, 2, 3]) B = np.array([4, 5, 6]) # ドット積の計算 dot_product = np.dot(A, B) # ノルムの計算 norm_A = np.linalg.norm(A) norm_B = np.linalg.norm(B) print("norm_A:",norm_A) print("norm_B:",norm_B) # コサイン類似度の計算 cosine_similarity = dot_product / (norm_A * norm_B) print("cosine_similarity:",cosine_similarity) #norm_A: 3.7416573867739413 #norm_B: 8.774964387392123 #cosine_similarity: 0.9746318461970762 |
４．コレクションデータ型とメソッド
４．１ リスト (List)
リストは、順序付けられた変更可能なコレクションです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
# -*- coding: utf-8 -*- import numpy as np # リストの作成 my_list = [1, 2, 3, 4, 5] # 要素の追加 my_list.append(6) print(my_list) # 出力: [1, 2, 3, 4, 5, 6] # 要素の挿入 my_list.insert(2, 2.5) print(my_list) # 出力: [1, 2, 2.5, 3, 4, 5, 6] # 要素の削除 my_list.remove(2.5) print(my_list) # 出力: [1, 2, 3, 4, 5, 6] # 要素のポップ（削除と取得） last_element = my_list.pop() print(last_element) # 出力: 6 print(my_list) # 出力: [1, 2, 3, 4, 5] # インデックスの取得 index = my_list.index(3) print(index) # 出力: 2 # ソート my_list.sort() print(my_list) # 出力: [1, 2, 3, 4, 5] # リバース my_list.reverse() print(my_list) # 出力: [5, 4, 3, 2, 1] |
４．２ タプル (Tuple)
タプルは、順序付けられた変更不可能なコレクションです。
|
1 2 3 4 5 6 7 8 9 10 11 |
# -*- coding: utf-8 -*- import numpy as np # タプルの作成 my_tuple = (1, 2, 3, 4, 5) # 要素のアクセス second_element = my_tuple[1] print(second_element) # 出力: 2 # タプルは変更不可能なので要素の追加や削除はできない |
４．３ セット (Set)
集合セットは重複しない要素（同じ値ではない要素、ユニークな要素）のコレクションで、和集合・差集合・積集合などの集合演算を行うことができます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
# -*- coding: utf-8 -*- import numpy as np # 二つのセットの定義 set1 = {1, 2, 3, 4, 5} set2 = {4, 5, 6, 7, 8} # 和集合の計算 union_set = set1.union(set2) print("Union:", union_set) # 出力: Union: {1, 2, 3, 4, 5, 6, 7, 8} union_set = set1 | set2 #短縮記法 print("Union:", union_set) # 出力: Union: {1, 2, 3, 4, 5, 6, 7, 8} # 差集合の計算 (set1 - set2) difference_set = set1.difference(set2) print("Difference (set1 - set2):", difference_set) # 出力: Difference (set1 - set2): {1, 2, 3} difference_set = set1 - set2 #短縮記法 print("Difference (set1 - set2):", difference_set) # 出力: Difference (set1 - set2): {1, 2, 3} # 差集合の計算 (set2 - set1) difference_set_rev = set2.difference(set1) print("Difference (set2 - set1):", difference_set_rev) # 出力: Difference (set2 - set1): {8, 6, 7} difference_set_rev = set2 - set1 #短縮記法 print("Difference (set2 - set1):", difference_set_rev) # 出力: Difference (set2 - set1): {8, 6, 7} # 積集合の計算 intersection_set = set1.intersection(set2) print("Intersection:", intersection_set) # 出力: Intersection: {4, 5} intersection_set = set1 & set2 #短縮記法 print("Intersection:", intersection_set) # 出力: Intersection: {4, 5} |
Union: {1, 2, 3, 4, 5, 6, 7, 8}
Union: {1, 2, 3, 4, 5, 6, 7, 8}
Difference (set1 – set2): {1, 2, 3}
Difference (set1 – set2): {1, 2, 3}
Difference (set2 – set1): {8, 6, 7}
Difference (set2 – set1): {8, 6, 7}
Intersection: {4, 5}
Intersection: {4, 5}
４．４ ディクショナリ (Dictionary)
ディクショナリは、キーと値のペアのコレクションです。順序はPython 3.7以降で保持されます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# -*- coding: utf-8 -*- import numpy as np # ディクショナリの作成 my_dict = {'a': 1, 'b': 2, 'c': 3} # 要素の追加と更新 my_dict['d'] = 4 my_dict['a'] = 10 print(my_dict) # 出力: {'a': 10, 'b': 2, 'c': 3, 'd': 4} # 要素の削除 del my_dict['b'] print(my_dict) # 出力: {'a': 10, 'c': 3, 'd': 4} # キーの取得 keys = my_dict.keys() print(keys) # 出力: dict_keys(['a', 'c', 'd']) # 値の取得 values = my_dict.values() print(values) # 出力: dict_values([10, 3, 4]) # キーと値の取得 items = my_dict.items() print(items) # 出力: dict_items([('a', 10), ('c', 3), ('d', 4)]) # 特定のキーの値を取得 value_a = my_dict.get('a') print(value_a) # 出力: 10 |
{‘a’: 10, ‘b’: 2, ‘c’: 3, ‘d’: 4}
{‘a’: 10, ‘c’: 3, ‘d’: 4}
dict_keys([‘a’, ‘c’, ‘d’])
dict_values([10, 3, 4])
dict_items([(‘a’, 10), (‘c’, 3), (‘d’, 4)])
10
４．５ デフォルトディクショナリ (defaultdict)
defaultdict は、キーが存在しない場合にデフォルト値を提供するディクショナリです。
このデフォルト値を生成するために使用されるのがファクトリ関数です。
defaultdict を使用するには、collections モジュールをインポートし、デフォルト値を生成するためのファクトリ関数を渡してインスタンスを作成します。
ファクトリ関数として、いくつかの組み込み関数や独自に定義した関数を使用できます。
・int：デフォルト値として0を返す
・list：デフォルト値として空のリストを返す
・set：デフォルト値として空のセットを返す
defaultdict(, {‘a’: 1})
defaultdict(, {‘a’: [1]})
defaultdict(, {‘a’: {1}})
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# -*- coding: utf-8 -*- import numpy as np from collections import defaultdict # ファクトリ関数として int を渡すと、デフォルト値が 0 になる default_dict = defaultdict(int) # 存在しないキーにアクセスすると、デフォルト値が返される print(default_dict['a']) # 出力: 0 # 値を設定する default_dict['a'] += 1 print(default_dict) # 出力: defaultdict(<class 'int'>, {'a': 1}) # デフォルト値として空のリストを返すファクトリ関数 list_dict = defaultdict(list) list_dict['a'].append(1) print(list_dict) # 出力: defaultdict(<class 'list'>, {'a': [1]}) # デフォルト値として空のセットを返すファクトリ関数 set_dict = defaultdict(set) set_dict['a'].add(1) print(set_dict) # 出力: defaultdict(<class 'set'>, {'a': {1}}) |
４．６ デキュー (deque)
deque は、両端での高速な挿入と削除が可能なデータ構造です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# -*- coding: utf-8 -*- import numpy as np from collections import deque # デキューの作成 dq = deque([1, 2, 3, 4, 5]) # 要素の追加 dq.append(6) dq.appendleft(0) print(dq) # 出力: deque([0, 1, 2, 3, 4, 5, 6]) # 要素の削除 dq.pop() dq.popleft() print(dq) # 出力: deque([1, 2, 3, 4, 5]) |
deque([0, 1, 2, 3, 4, 5, 6])
deque([1, 2, 3, 4, 5])
５．データ構造の操作
５．１ インデックス参照（スライス）
リスト、タプル、文字列、辞書、セット、Numpy配列などのデータ構造を操作するための基本的な方法です。これにより、特定の要素へのアクセス、更新、部分列の取得が可能になります。
Pythonのスライスは、[start:stop:step] の形式で指定します。
start: スライスの開始位置（この位置の要素を含む）
stop: スライスの終了位置（この位置の要素を含まない）
step: スライスのステップ
以下に、スライスの基本的な使い方と例を示します。
（１）リストのスライス
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# -*- coding: utf-8 -*- import numpy as np # リストのスライス arr = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] # インデックス2からインデックス5までの要素を取得 print(arr[2:6]) # [2, 3, 4, 5] # インデックス0からインデックス5までの要素を2ステップずつ取得 print(arr[0:6:2]) # [0, 2, 4] # インデックス5以降の要素を取得 print(arr[5:]) # [5, 6, 7, 8, 9] # インデックス5以前の要素を取得 print(arr[:5]) # [0, 1, 2, 3, 4] # すべての要素を2ステップずつ取得 print(arr[::2]) # [0, 2, 4, 6, 8] # 逆順に取得 print(arr[::-1]) # [9, 8, 7, 6, 5, 4, 3, 2, 1, 0] |
[2, 3, 4, 5]
[0, 2, 4]
[5, 6, 7, 8, 9]
[0, 1, 2, 3, 4]
[0, 2, 4, 6, 8]
[9, 8, 7, 6, 5, 4, 3, 2, 1, 0]
（２）文字列のスライス
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# -*- coding: utf-8 -*- import numpy as np s = "Hello, World!" # インデックス0からインデックス5までの文字を取得 print(s[0:5]) # "Hello" # インデックス7以降の文字を取得 print(s[7:]) # "World!" # 逆順に取得 print(s[::-1]) # "!dlroW ,olleH" |
Hello
World!
!dlroW ,olleH
（３）１次元配列のスライス
|
1 2 3 4 5 6 7 8 9 10 |
# -*- coding: utf-8 -*- import numpy as np arr = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) # インデックス2からインデックス5までの要素を取得 print(arr[2:6]) # [2 3 4 5] # インデックス0からインデックス5までの要素を2ステップずつ取得 print(arr[0:6:2]) # [0 2 4] |
[2 3 4 5]
[0 2 4]
（４）２次元配列のスライス
|
1 2 3 4 5 6 7 8 9 10 |
# -*- coding: utf-8 -*- import numpy as np arr = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) # インデックス2からインデックス5までの要素を取得 print(arr[2:6]) # [2 3 4 5] # インデックス0からインデックス5までの要素を2ステップずつ取得 print(arr[0:6:2]) # [0 2 4] |
[2 3 4 5]
[0 2 4]
（５）３次元配列のスライス
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
# -*- coding: utf-8 -*- import numpy as np # 3次元配列 tensor = np.array([ [[ 0, 1, 2], [ 3, 4, 5], [ 6, 7, 8]], [[ 9, 10, 11], [12, 13, 14], [15, 16, 17]], [[18, 19, 20], [21, 22, 23], [24, 25, 26]] ]) # 1番目と2番目の「スライス」を取得（最初の2つの「面」） print(tensor[:2]) # [[[ 0 1 2] # [ 3 4 5] # [ 6 7 8]] # # [[ 9 10 11] # [12 13 14] # [15 16 17]]] # 各「面」の最初の2行を取得 print(tensor[:, :2]) # [[[ 0 1 2] # [ 3 4 5]] # # [[ 9 10 11] # [12 13 14]] # # [[18 19 20] # [21 22 23]]] # 各「面」のすべての行と最初の2列を取得 print(tensor[:, :, :2]) # [[[ 0 1] # [ 3 4] # [ 6 7]] # # [[ 9 10] # [12 13] # [15 16]] # # [[18 19] # [21 22] # [24 25]]] |
（６）スライスオブジェクト
スライスオブジェクトはPythonのslice型で、スライスの開始、終了、およびステップを格納します。
|
1 2 3 4 5 6 7 8 9 |
# -*- coding: utf-8 -*- import numpy as np arr = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] slice_obj = slice(2, 6) print(arr[slice_obj]) # [2, 3, 4, 5] slice_obj = slice(0, 6, 2) print(arr[slice_obj]) # [0, 2, 4] |
[2, 3, 4, 5]
[0, 2, 4]