畳み込み

１．畳み込みとは
　畳み込み（たたみこみ、英: Convolution）とは、２つの関数を合わせて新しい関数を作る数学的な操作です。主に信号処理や画像処理、機械学習（特に畳み込みニューラルネットワーク、CNN）で広く使用されます。
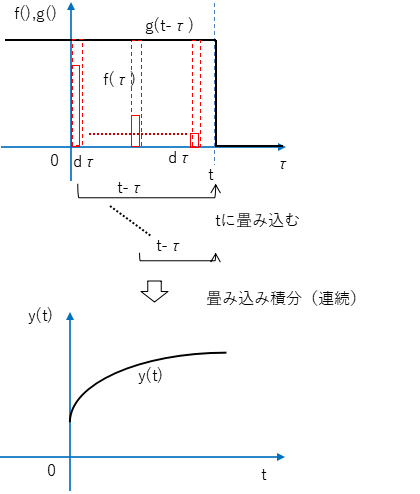
　畳み込みの基本的な概念を理解するために、１次元の畳み込みについて説明します。２つの関数fとgの連続的な畳み込み（畳み込み積分）は、以下のように定義されます。

２．連続的な畳み込み（畳み込み積分）
　畳み込みは２つの関数を操作して新しい関数を生成する数学的な操作です。

畳み込みを視覚的に理解するために、例として、次の関数の畳み込みを考えます。

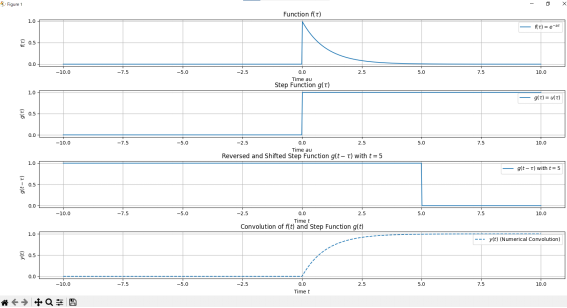
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad

# Parameters
t = np.linspace(-10, 10, 800)  # Time range
tau_shift = 5  # Shift for the g(τ - t) plot
a = 1  # Parameter for the exponential function

# Define the functions
def f(t, a):
    return np.exp(-a * t) * (t >= 0)

def g(t):
    return np.heaviside(t, 1)

# Numerical convolution using scipy's quad
def numerical_convolution(t, a):
    result = np.zeros_like(t)
    for i in range(len(t)):
        if t[i] >= 0:
            result[i], _ = quad(lambda tau: f(tau, a) * g(t[i] - tau), 0, t[i])
    return result

# Compute the functions
f_tau = f(t, a)
g_tau = g(t)
y_t = numerical_convolution(t, a)

# Compute g(τ - t)
g_tau_t = g(tau_shift - t)

# Plot the functions
plt.figure(figsize=(10, 10))

# Plot f(τ)
plt.subplot(4, 1, 1)
plt.plot(t, f_tau, label=r'$f(\tau) = e^{-a\tau}$')
plt.xlabel('Time $\tau$')
plt.ylabel(r'$f(\tau)$')
plt.title(r'Function $f(\tau)$')
plt.legend()
plt.grid(True)

# Plot g(τ)
plt.subplot(4, 1, 2)
plt.plot(t, g_tau, label=r'$g(\tau) = u(\tau)$')
plt.xlabel('Time $\tau$')
plt.ylabel(r'$g(\tau)$')
plt.title(r'Step Function $g(\tau)$')
plt.legend()
plt.grid(True)

# Plot g(τ - t)
plt.subplot(4, 1, 3)
plt.plot(t, g_tau_t, label=r'$g(\tau - t)$ with $\tau = ' + str(tau_shift) + r'$')
plt.xlabel('Time $t$')
plt.ylabel(r'$g(\tau - t)$')
plt.title(r'Reversed and Shifted Step Function $g(\tau - t)$ with $\tau = ' + str(tau_shift) + r'$')
plt.legend()
plt.grid(True)

# Plot y(t) (Convolution result)
plt.subplot(4, 1, 4)
plt.plot(t, y_t, label=r'$y(t)$ (Numerical Convolution)', linestyle='--')
plt.xlabel('Time $t$')
plt.ylabel('$y(t)$')
plt.title(r'Convolution of $f(t)$ and Step Function $g(t)$')
plt.legend()
plt.grid(True)

# Adjust layout
plt.tight_layout()
plt.show()

３．離散的な畳み込み（畳み込み和）

y=[0. 1. 2.5 4. 5.5 7. 2.5]

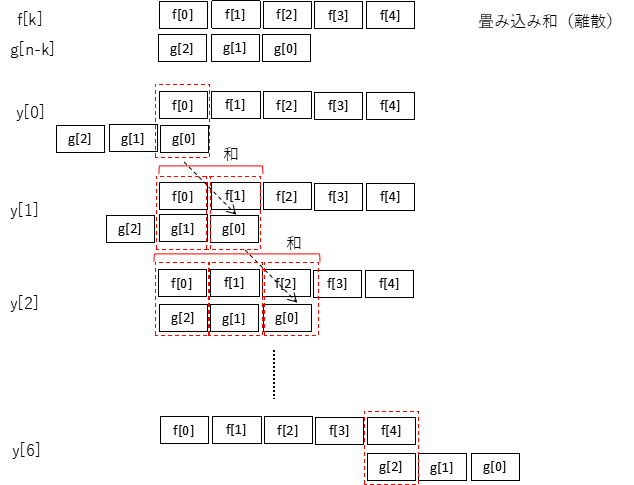
# -*- coding: utf-8 -*-
import numpy as np

f = np.array([1, 2, 3, 4, 5])
g = np.array([0, 1, 0.5])

# 畳み込みの計算
conv_result = np.convolve(f, g, mode='full')
print(conv_result)