1.概要
トランスフォーマーの元となるアーキテクチャは、以下の論文で発表されました:
Title: Attention Is All You Need
Authors: Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez,
Łukasz Kaiser, and Illia Polosukhin
Published in: NeurIPS 2017 (Conference on Neural Information Processing Systems)
ChatGPTなどの自然言語処理、画像生成などモデルとして使用されて、主な特徴を以下に示します。
(1)自己注意機構(Self-Attention Mechanism)
自己注意機構は、入力シーケンス(文章など)の各要素(トークン)のシーケンス全体の他の要素に対する重要性を評価する方法です。これにより、文中の単語同士の関係を捉えることができるようになり、文章の生成において、次に続く単語の選択するときの重みづけ(文脈によって動的に変化する)ができるようになります。
(2)位置エンコーディング(Positional Encoding)
トランスフォーマーはリカレント(再帰的)な構造を持たないため、入力シーケンスの順序情報を明示的にモデルに提供する必要があります。位置エンコーディングはこの問題を解決するために使用されます。
(3)エンコーダ・デコーダ構造(Encoder-Decoder Structure)
トランスフォーマーモデルはエンコーダとデコーダの2つの主要部分から構成されています。エンコーダーは、入力された文章を固定長のベクトル(文脈ベクトル)に変換する役割をもちます。デコーダはエンコーダーが生成した文脈ベクトルを元に推論した結果(出力)を生成する役割をもちます。
(4)並列計算の効率性
トランスフォーマーは並列計算に適しており、従来のRNN(Recurrent Neural Networks)やLSTM(Long Short-Term Memory)に比べてトレーニング速度が速いという利点があります。これは特に大規模なデータセットでの学習においてメリットとなります。
(5)スケーラビリティ
トランスフォーマーは非常に大規模なモデルにスケールさせることができ、多くのパラメータを持つことで高い表現力を持っています。例えば、BERTやGPTなどの大規模なトランスフォーマーモデルは数億から数十億のパラメータを持ち、非常に高い性能を発揮します。
(6)多用途性
トランスフォーマーは機械翻訳、テキスト生成、要約、質問応答、画像認識など、さまざまなタスクに適用可能です。これは、トランスフォーマーがシーケンスの関係性をうまく捉えることができるためです。
2.トランスフォーマーの構成
以上の特徴をモデルの各部分について考察していきます。
大まかにトランスフォーマーはエンコーダーとデコーダに分けられます。エンコーダで入力データを埋め込みベクトル空間に変換します。
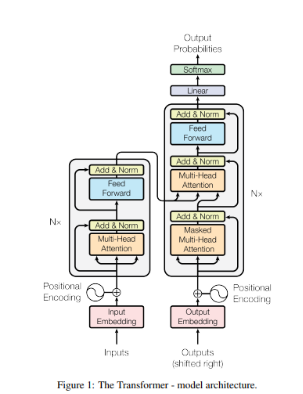
arXiv:170 2 Aug 2023「Attention Is All You Need」から引用
文章の生成を行う場合を例に、エンコーダーとデコーダの働きについて見ていきます。
2.1 エンコーダーの働き
Inputsで文章を入力し、入力済みの文章に続く単語(トークン)の予測の基となるベクトルを作成するまでがエンコーダーの機能となります。
Inputsから順番に見ていきます。
①InputsとinputEmbedding
文章を構成する全ての単語を事前学習したEmbededdingのデータで数値ベクトルに変換します。これを埋め込みベクトルといいます。ここでは単語から一意的にEmbededdingのデータに置き換えるだけで文脈は考慮されていません。
②PositionalEncoding
①のinputの文章の各単語をEmbeddingベクトル空間に置き換えたベクトルデータに対して、文脈上の単語の位置情報を加えます。
(位置エンコーディングの計算方法)
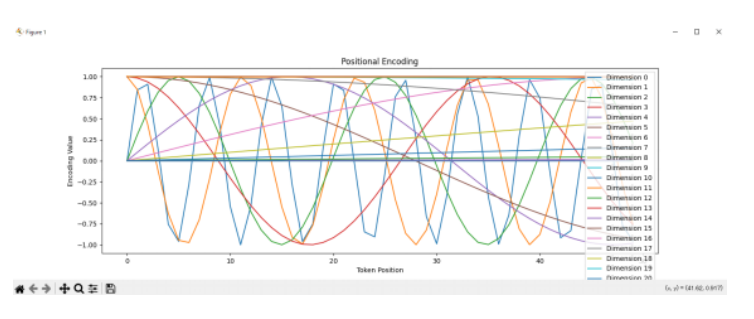
位置エンコーディングは、サイン関数とコサイン関数を使用して計算されます。具体的には、次のような形で各次元ごとに計算されます:

この位置エンコーディングにおける各次元は、異なる周期や位相を持つ関数の値を表し、第一次元は高周波で周期的な情報を担い、第二次元は低周波で周期的な情報を担うといった役割をします。
③Multi-HeadAttention
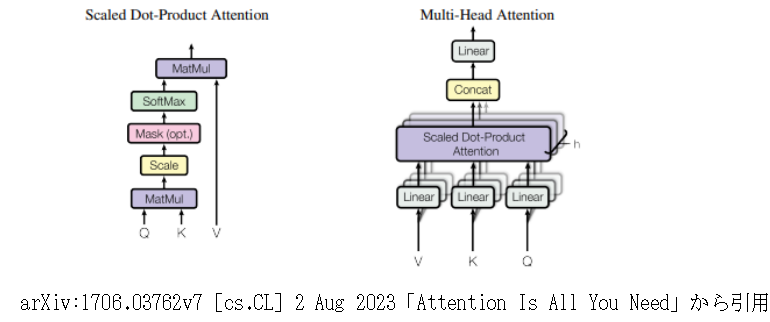
(a)入力ベクトルV、K、Qの準備
入力シーケンスを受け取り、Query(Q)、Key(K)、Value(V)を生成します
(b)Linear変換
Linear変換は、Q、K、Vそれぞれに対して線形変換(入力ベクトルに重み行列を掛け合わせ、バイアスベクトルを加える操作)を適用し、新しいQ’、K’、V’を得ます。線形変換は以下の式で表されます

Multi-Head Attentionでは、以下のようにQuery、Key、Valueそれぞれに異なる重み行列を適用します。

(c)ScaledDot-ProductAttention
ScaledDot-ProductAttentionは、Queryベクトル(入力シーケンスで注意を払う単語)と入力シーケンスの他の要素のKeyベクトル、Valueベクトルから下記の計算により、スコアを求めます。
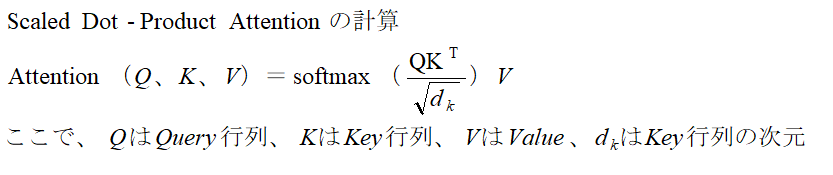
Scaled Dot-Product Attentionの出力は、入力のValue行列Vと同じ形状を持ちます。
具体的には、出力の形状はVの形状(バッチサイズ、シーケンス長、埋め込み次元)と一致します。
Multi-Head Attention機構においてはこれらの処理はヘッドが複数あり、各ヘッドは異なる部分空間(埋め込みベクトルの異なる次元)で独自のScaled Dot-Product Attentionを計算し、その結果を結合して最終的な出力を生成します。例として、埋め込み次元が8でヘッド数が4のときは各ヘッドの次元は8/4=2となります。
(c)Concat
各ヘッドの出力を結合し、最終的な出力を得ます。
④Add&Norm
(a)Add(残差接続)
勾配消失問題を軽減し、トレーニングの安定性を高めるため入力(Query)をその層の出力に直接足し合わせます。
Output=Layer Output+Input(ここではQuery)
(b)Norm(正規化)
正規化は各層の出力のスケールを調整しトレーニングの安定性と収束速度を向上させます。
⑤Feedward
フィードフォワードニューラルネットワーク(Feedforward Neural Network、FFN)は、トランスフォーマーモデルの各エンコーダーおよびデコーダーブロック内で、トークンごとの情報を変換し、特徴抽出や複雑なパターンを学習するためのものです。自己注意機構が各トークン間の相関を捉えるのに対して、FFNは各トークンの特徴を独立に変換し、より高度な特徴を学習する役割を担います。具体的には最初の線形変換で高次元に変換し、非線形活性化関数を適用し、最後に線形変換で元の次元に戻します。
⑥Add&Norm
(a)Add(残差接続)
勾配消失問題を軽減し、トレーニングの安定性を高めるため入力(Query)をその層の出力に直接足し合わせます。
Output=Layer Output+Input(ここではQuery)
(b)Norm(正規化)
正規化は各層の出力のスケールを調整しトレーニングの安定性と収束速度を向上させます。
2.2 デコーダの働き
トランスフォーマーモデルのデコーダは、エンコーダから得られたコンテキスト情報をもとに、逐次的に出力シーケンスを生成する役割を担います
①OutputsとOutputsEmbedding
現在までに生成された部分シーケンスのトークンをベクトル表現に変換したものです。通常、これらのベクトルはEmbedding層を通じて得られます。
Embedding層は、語彙内の各トークンを固定次元の連続値ベクトルにマッピングします。
②PositionalEncoding
①のoutputの文章の各単語をEmbeddingベクトル空間に置き換えたベクトルデータに対して、文脈上の単語の位置情報を加えます。
位置ベクトルの計算方法は2.1項と同じです。
③Masked Multi-Head Attention
Masked Multi-Head Attention (Masked MHA) は、トランスフォーマーのデコーダで使用される自己注意機構の一部です。マスク付き自己注意機構は、未来の情報を見ないようにするためにマスクを適用します。

④Multi-Head Attention
デコーダのMulti-Head Attentionの入力にエンコーダからの出力が入っている理由は、エンコーダが入力シーケンスの各トークンの特徴を含むコンテキスト情報を提供するためです。これにより、デコーダは現在生成しているトークンが入力シーケンスのどの部分と関係しているかを学習できます。
⑤Linear
デコーダの出力は、通常、トークンの埋め込み次元を持つベクトルです。このベクトルを、単語サイズの次元に変換する必要があります。線形層は、デコーダの出力ベクトルに対して線形変換を適用し、単語サイズに対応するスコアベクトルを生成します。
⑥softmax
線形層からの出力のスコアにソフトマックス関数を適用することで確率分布に変換します。ソフトマックス関数は、各スコアを指数関数的に変換し、全体のスコアの合計が1になるように正規化します。
3.サンプル
トランスフォーマーのモデルを簡略化したエンコーダデコーダモデル(下記のブロック図)について実装し、確認を行います。
import numpy as np
# 単語の初期化
vocab = ["りんご", "赤い", "みかん", "黄色い", "の", "色", "は"]
inv_vocab = {i: word for i, word in enumerate(vocab)}
# 手動で設定されたエンベディングベクトル
embeddings = {
"りんご": np.array([0.8, 0.0, 0.8, 0.2]),
"赤い": np.array([0.8, 0.5, 0.8, 0.2]),
"みかん": np.array([0.1, 0.9, 0.1, 0.8]),
"黄色い": np.array([0.3, 0.8, 0.3, 0.8]),
"の": np.array([0.2, 0.3, 0.1, 0.2]),
"色": np.array([0.3, 0.2, 0.2, 0.3]),
"は": np.array([0.1, 0.2, 0.2, 0.2])
}
# エンコーダの入力
encoder_input = ["りんご", "の", "色","は"]
# デコーダの入力
decoder_input = encoder_input
# 単語を埋め込みベクトルに変換
def embed_sequence(sequence):
return np.array([embeddings[word] for word in sequence])
# 位置エンコーディングの生成
def positional_encoding(sequence_length, d_model):
position = np.arange(sequence_length)[:, np.newaxis]
div_term = np.exp(np.arange(0, d_model, 2) * -(np.log(10000.0) / d_model))
pe = np.zeros((sequence_length, d_model))
pe[:, 0::2] = np.sin(position * div_term)
pe[:, 1::2] = np.cos(position * div_term)
return pe
# マルチヘッドアテンション
def multi_head_attention(Q, K, V, num_heads):
def attention(Q, K, V):
d_k = Q.shape[-1]
scores = np.dot(Q, K.T) / np.sqrt(d_k)
weights = softmax(scores)
print("weights:",weights,"V:",V)
return np.dot(weights, V)
d_model = Q.shape[-1]
head_dim = d_model // num_heads
heads = []
for i in range(num_heads):
Q_i = Q[:, i*head_dim:(i+1)*head_dim]
print("i:",i,"Q_i:",Q_i)
K_i = K[:, i*head_dim:(i+1)*head_dim]
V_i = V[:, i*head_dim:(i+1)*head_dim]
heads.append(attention(Q_i, K_i, V_i))
print("④i:",i,"heads:",heads)
return np.concatenate(heads, axis=-1) #ヘッドの出力を次元(埋め込みベクトルの次元)に沿って結合
# ソフトマックス関数
def softmax(x):
exp_x = np.exp(x - np.max(x, axis=-1, keepdims=True))
return exp_x / np.sum(exp_x, axis=-1, keepdims=True)
# エンコーダ
def encoder(encoder_input_emb, num_heads):
print("# エンコーダのセルフアテンション")
encoder_self_attention =multi_head_attention(encoder_input_emb, encoder_input_emb, encoder_input_emb, num_heads)
print("encoder_self_attention:",encoder_self_attention)
return encoder_self_attention
# デコーダ
def decoder(decoder_input_emb, encoder_output, num_heads):
print("# デコーダのセルフアテンション")
decoder_self_attention = multi_head_attention(decoder_input_emb, decoder_input_emb, decoder_input_emb, num_heads)
print("decoder_self_attention:",decoder_self_attention)
print("# エンコーダ-デコーダアテンション")
encoder_decoder_attention = multi_head_attention(decoder_self_attention, encoder_output, encoder_output, num_heads)
print("encoder_decoder_attention:",encoder_decoder_attention)
return encoder_decoder_attention
# 埋め込みに変換
encoder_input_emb = embed_sequence(encoder_input)
print("①encoder_input_emb:",encoder_input_emb)
decoder_input_emb = embed_sequence(decoder_input)
print("①'decoder_input_emb:",decoder_input_emb)
# 位置エンコーディングの追加
## 位置エンコーディングの生成
encoder_pos_enc = positional_encoding(len(encoder_input), encoder_input_emb.shape[1])
print("②encoder_pos_enc:",encoder_pos_enc)
decoder_pos_enc = positional_encoding(len(decoder_input), decoder_input_emb.shape[1])
print("②'decoder_pos_enc:",decoder_pos_enc)
## 埋め込みベクトルに位置ベクトルを加算
encoder_input_emb += encoder_pos_enc
print("③encoder_input_emb:",encoder_input_emb)
decoder_input_emb += decoder_pos_enc
print("③'decoder_input_emb:",decoder_input_emb)
# エンコーダとデコーダの出力
num_heads = 2
encoder_output = encoder(encoder_input_emb, num_heads)
print("⑤encoder_output:",encoder_output)
decoder_output = decoder(decoder_input_emb, encoder_output, num_heads)
print("⑥decoder_output:",decoder_output)
# 次の単語の予測
def predict_next_word(decoder_output, embeddings, inv_vocab):
last_output = decoder_output[-1] # デコーダの出力の最後のベクトル
print("last_output:",last_output)
similarities = np.dot(np.array(list(embeddings.values())), last_output)
print("similarities:",similarities)
return inv_vocab[np.argmax(similarities)]
next_word = predict_next_word(decoder_output, embeddings, inv_vocab)
print("次に来る単語は:", next_word)・前提条件
単語のエンベディングベクトルは回答が合うように手動で設定した
embeddings = {
“りんご”: np.array([0.8, 0.0, 0.8, 0.2]),
“赤い”: np.array([0.8, 0.5, 0.8, 0.2]),
“みかん”: np.array([0.1, 0.9, 0.1, 0.8]),
“黄色い”: np.array([0.3, 0.8, 0.3, 0.8]),
“の”: np.array([0.2, 0.3, 0.1, 0.2]),
“色”: np.array([0.3, 0.2, 0.2, 0.3]),
“は”: np.array([0.1, 0.2, 0.2, 0.2])
}
・実行環境
Windows 10 Pro
Python 3.12.4
numpy 1.26.4
・実行結果
:
similarities: [1.23933206 1.39950039 1.39310835 1.60962455 0.5542311 0.76903867
0.46902724]
次に来る単語は: 黄色い #単語の4番目
(パラメータ数)
(計算例)
ボキャブラリサイズ:7
エンベデイングサイズ:4
マルチヘッドアッテンションのヘッド数:2
エンコーダのマルチヘッドアッテンション層:1
デコーダのマルチヘッドアッテンション層:2
のときのパラメータ数を求める
1.エンベディング層のパラメータ数
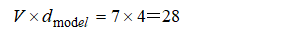
2.マルチヘッドアテンション層のパラメータ数

3.フィードフォワードネットワーク層のパラメータ数(サンプルでは省略)
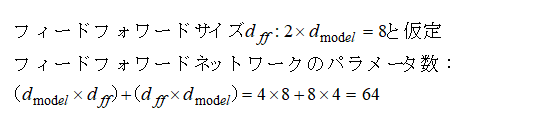
4.エンコーダ層のパラメータ数
エンコーダ層はマルチヘッドアテンション層1つとフィードフォワード層1つ(仮定)を持ちます。
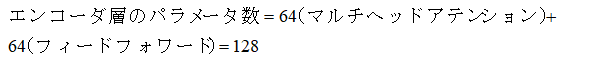

次に処理の順番に各ベクトルのパラメータの変化を示します。